| 文章 | 会议 | 等级 | 阅读情况 |
|---|---|---|---|
| Accelerating Multi-Scalar Multiplication for Efficient Zero Knowledge Proofs with Multi-GPU Systems2024 | ASPLOS 2024 | CCF-A | [] |
GZKP: A GPU Accelerated Zero-Knowledge Proof System
2023 - 5
并行化方法
称把一个桶的点加起来的计算位一个点合并任务。将多个点合并任务分配到一个block上。每个点合并任务都分配一个warp。
其中,warp内使用合作组(cooperative groups)来并行执行点加运算。同一个warp会被拆分为多个合作组,每个合作组都独立执行点加运算。
考虑到不同点合并任务的负载(点的个数)不同,文章会按照任务负载将任务分配到不同的blcok上,一个block可能会被分配多个任务。
预计算
与其于把各个window分开计算并最后通过window reduction合并到一起,本文预先计算了每个点在各个windows下经过对应偏移量的值(i.e. 乘以对应窗口的系数)。如此操作过后,不同窗口但标量相同的点就可以使用同一个桶了。从而增大了单个桶的大小,去除了窗口合并时的点乘。
核心原理:
原来的Pippenger计算方法为把标量$k_i$按位分块,从而把原本完整的MSM计算拆分位多个在不同位上的MSM子问题(窗口),如下公式所示。
$$\sum k_i \cdot P_i = \sum_j 2^{(j-1) \cdot S} \sum_i k_{ij} \cdot P_i$$
其中,$S$为每个子问题位长,$k_{ij}$表示第$i$个标量的第$j$段。
上式可以变为:
$$\sum_j \sum_i k_{ij} \cdot (2^{j-1} \cdot P_i)$$
考虑到对于固定问题的ZKP,其$P_i$是在不同批次的MSM中保持不变的,变的只有标量,故预计算只需要进行一次即可。
但是预计算需要存储巨量的点在显存中,会造成巨大的显存压力。故文章是分段预计算的,没有被预计算覆盖过的点需要在点合并的时候找到最近的有预计算的点,再点乘相应的位数后才能被加到桶中。
有限域计算优化
不只是运用SM上的整数计算单元,把浮点计算单元也利用上以共同执行大整数计算。
Load-Balanced Parallel Implementation on GPUs for Multi-Scalar Multiplication Algorithm
2024 - 3
朴素方法分析
double-and-add方法

需要计算$n\lambda$次PADD与$\lambda -1$次PDBL,其中$\lambda$为椭圆曲线群所在的有限域阶数的二进制位数。
Pippenger
$\lceil \frac{\lambda}{c} \rceil (n + 2^{c+1} - 3)$次PADD及$c(\lceil \frac{\lambda}{c} \rceil - 1)$次PDBL,其中$c$为窗口位数。
并行化方法
点合并阶段
每个block处理一个窗口(pippenger子问题),每个thread处理固定范围的连续点:$\left[threadid \cdot \lceil n / N \rceil, (threadid + 1) \cdot \lceil n / N \rceil \right)$。计算完的结果会被存放到一个不会冲突的全局内存中(下解释)
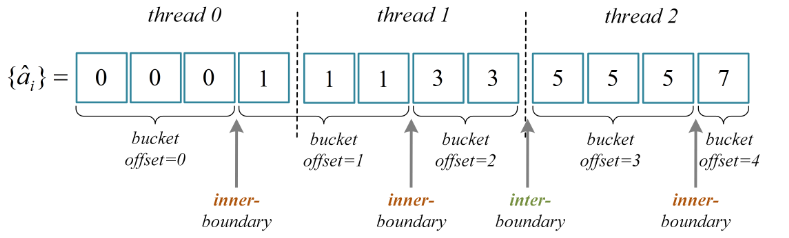
考虑到不同的标量可能会跨过每个线程分管的范围,若所有线程直接公用同一个global memory存放结果,势必会造成冲突:如上图所示($a_i$表示标量(pippenger分块过后的)),线程0和线程1均分别计算了标量为1的部分桶。文章分配了一个较大的全局内存并采用了一种偏移机制来避免这个问题。
$$offset_{tid} = tid + min\left[ \left\lceil \frac{a_i + 1}{2} \right\rceil \right]$$
式中,$tid$为线程id,$offset_{tid}$表示每个线程写bukkit位置的起始偏移量。显然对于某个线程,前面至少有$tid$个结果。后者考虑最坏情况下每个线程都是满的(aka每个标量都独自出现),原文用了一些标量变换的方法使得标量只有奇数的,故需要除以2后上取整。
记录下每个位置上放了什么bukkit,这个数组必然是单调递增的,可以采用二分查找的方法把分处于不同缓存区域的bukkit给加起来。
桶累积阶段
标量变换&预计算
原先每个$k_{i,j} \in [0, 2^c - 1]$,考虑到椭圆曲线上取反操作廉价,将原先的$k_{i,j}$变为有符号数$k’_{i,j} \in [- 2^{c-1} -1, 2^{c-1} -1]$,将大于等于$2^{c-1}$的标量变为负数,并将对应$P$取反。
PADD优化