1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
|
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<complex>
using namespace std;
typedef complex <double> cp;
const double PI=acos(-1);
const int M=100000+100;
const int N=8\*M;
inline cp omega(int K,int n)
{
return cp(cos(2\*PI\*K/n),sin(2\*PI\*K/n));
}
void FFT(cp a[],int n,bool type)
{
static int len=0,num=n-1,t[N];
while(num!=0) len++,num/=2;
for(int i=0,j;i<=n;i++)
{
for(j=0,num=i;j<len;j++)
t[j]=num%2,num/=2;
reverse(t,t+len);
for(j=0,num=0;j<len;j++)
num+=t[j]\*(1<<j);
if(i<num) swap(a[i],a[num]);
}
for(int l=2;l<=n;l\*=2)
{
int m=l/2;
cp x0=omega(1,l);
if(type==true) x0=conj(x0);
for(int j=0;j<n;j+=l)
{
cp x=cp(1,0);
for(int k=0;k<m;k++,x\*=x0)
{
cp temp=x\*a[j+k+m];
a[j+k+m]=a[j+k]-temp;
a[j+k]=a[j+k]+temp;
}
}
}
}
int n,m;
double q[N];
cp f[N],g[N],f2[N];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%lf",&q[i]);
for(int i=1;i<=n;i++)
g[i]=(1.0/i/i);
m=1;
while(m<2\*n) m\*=2;
for(int i=1;i<m;i++)
f[i]=q[i],f2[i]=q[i];
FFT(g,m,false);
FFT(f,m,false);
reverse(f2+1,f2+n+1);
FFT(f2,m,false);
for(int i=0;i<m;i++)
f[i]\*=g[i],f2[i]\*=g[i];
FFT(f,m,true);
FFT(f2,m,true);
for(int i=1;i<=n;i++)
printf("%lf\n",(f[i].real()-f2[n-i+1].real())/m);
return 0;
}
|
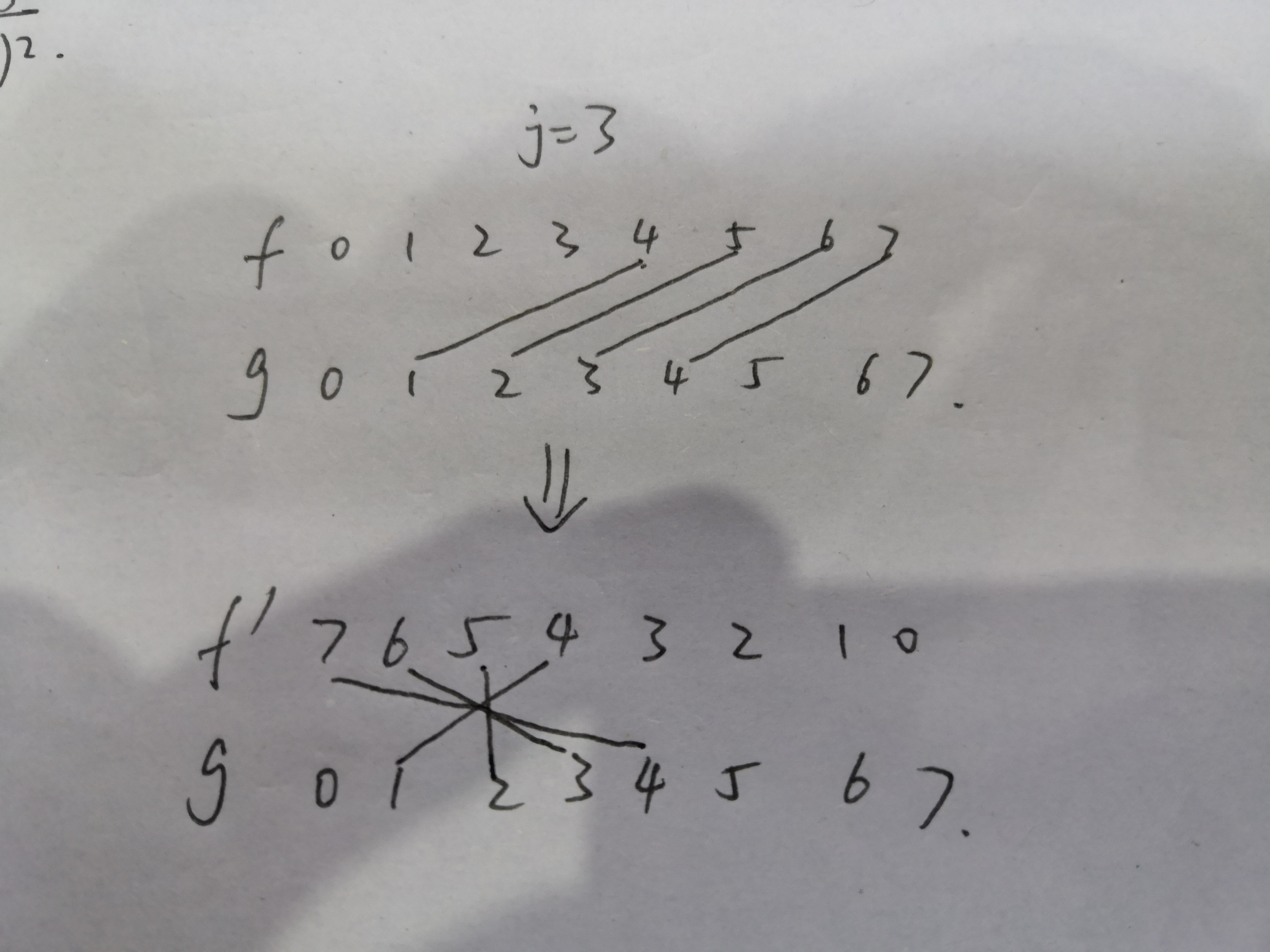 卷积用FFT快速计算即可 时间复杂度$O(nlogn)$
卷积用FFT快速计算即可 时间复杂度$O(nlogn)$



